Generate All Permutations of String without Duplicates (Python, Recursion)

Expected output

'abc' = ['abc', 'bac', 'bca', 'acb', 'cab', 'cba']

Solution 1

Try a few input and output samples manually.

P('a') = ['a']
P('ab') = ['ab', 'ba']
P('abc') = ['cab', 'acb', 'abc', 'cba', 'bca', 'bac']

Notice that to generate P('abc'), we take the output of P('ab') = ['ab', 'ba'] and try to append 'c' at each index/position 'ab' (begin, middle, end).

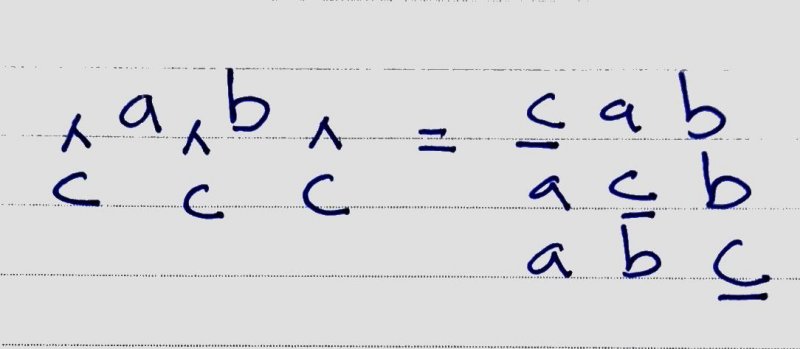
Recursion Insert

It seems like if we know the previous output P(n-1), we can generate the current output P(n). This sounds like a recursive solution.

def generate_permutations(text):    # validation    if text is None:        return None    # base, this is required as seeding value    if len(text) == 0:        return [""] # one empty element is required ensure the words loop run once    # else, we can seed with the following as well    '''    # if len(text) == 0: # base 0    #    return []    if len(text) == 1: # base 1        return [text]    '''    results = []    first = text[0]    remainder = text[1:]    words = generate_permutations(remainder)    # print(first, remainder, words)    for word in words:        for i in range(len(word)+1):            # insert first char at each index/position of word            s = word[:i] + first + word[i:]            results.append(s)    return results

Solution 2

P(a,b) = ab, ba
P(b,c) = bc, cb
P(a,c) = ac, ca

To generate P(a,b,c)

{ a +P(b,c) }  + { b + P(a,c) }  + { c + P(a,b) }

Observe that we need to try each character + P(remaining character).

def generate_permutations(text):    size = len(text)    results = []        # seed    if size == 0:        results.append("")        return results    # or    '''    # if size == 0:    #    return []    if size == 1:        return [text]    '''    for i in range(size): # loop each character        # generate str without current character (remaining character)        remainder = text[0:i] + text[i+1:]         # if text[i] = 'a', remainder = 'bc'        partials = generate_permutations(remainder)        # append current char to P(remaining character)        for s in partials:            results.append(text[i] + s)    return results

Big O Time:

How many time generate_permutation is called.

partials = generate_permutations(remainder)

For P('abc'), it is 3 * 2 * 1 = 3!, so it is O(n!) (since there is no caching/memoization, and n = n-1 = n)

for i in range(size)

We need to loop through each char in 'abc', so it is O(n * n!).

Based on Cracking the Coding Interview: 189 Programming Questions and Solutions by Gayle Laakmann McDowell.

Since we are calling permutation 0(n * n!) times (as an upper bound), and each one takes 0(n) time, the total runtime will not exceed O (n^2 * n!).

PS: It seems like I got O(n * n!) right, but the author also take into account string concatenation remainder = text[0:i] + text[i+1:] and print/append of result results.append(text[i] + s), which require O(n) in each node.

Solution 3

Observer the following diagram

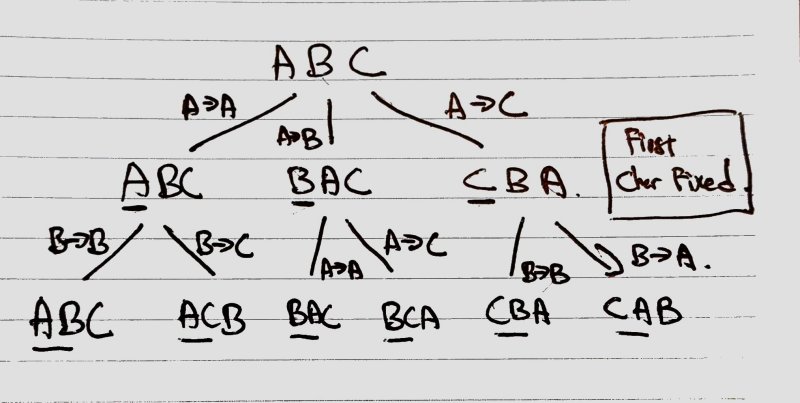
Recursion Permutation Swap

Level 0:
- Iterate a, b, c
- Swap char[first] with char[first], char[second], char[third]: a->a, a->b, a->c
- Fist character is done/fixed

Level 1:
- Iterate: it could be abc, bac or cba
- First character is done/fixed
- Swap char[second] with char[second], char[third]

Continue

def generate_permutation(text):    # convert string to list of char to allow swapping    _generate_permutation(list(text), 0, len(text)-1)def _generate_permutation(text, start, end):    # base    if start == end:        print(''.join(text))        return    for i in range(start, end+1):        text[start], text[i] = text[i], text[start]        _generate_permutation(text, start+1, end)        # backtrack like a tree, to restore previous state        text[start], text[i] = text[i], text[start]

Reference: https://www.geeksforgeeks.org/write-a-c-program-to-print-all-permutations-of-a-given-string/