Permutations With Repeating Characters (Python)

Generate permutations of n elements (including repeating/duplicate elements)

ab = aa, bb, ab, ba
abc = aaa, aab, abc ...

The number of combination should be n^k (n=number of elements, k=combination length). For this case, n and k happens to be the same.

ab = 2^2 = 4
abc = 3^3 = 9

If we use `abc`(n=3) to generate permutations of length 1 (k=1)
P(abc, 1) = a, b, c = 3^1 = 3 combinations

If we use `abc`(n=3) to generate permutations of length 2 (k=2)
P(abc, 2) = aa, bb, cc, ab, ac ... = 3^2 = 9 combinations

Linear iteration of all elements is unlikely to generate all combinations, so a recursive solution is more likely.

Imagine the following diagram.

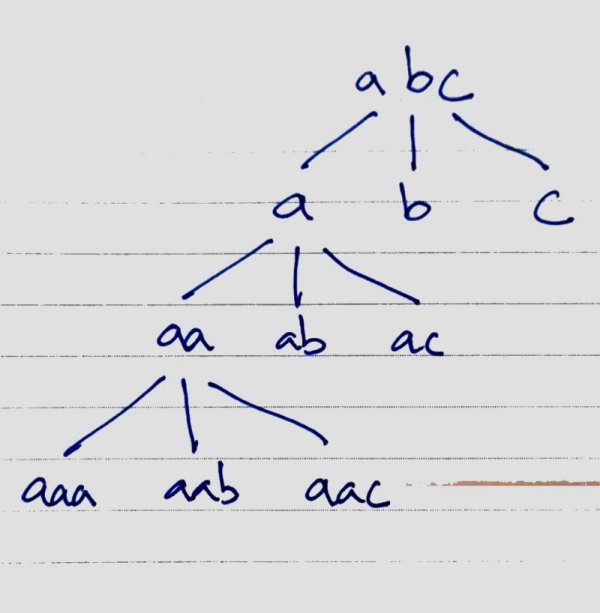
Recursion Permutation Repeat

Result of P(a) is used to generate P(ab). We start with a prefix of 1 character, then we more character to prefix until all combination are generated recursively.

def _permutation_repeat(text, prefix, n, k):    if k == 0: # base, len(prefix) == len(text)        print(prefix)        return    for i in range(n):        new_prefix = prefix + text[i] # a, aa, aaa, aab, aac ab, aba, abb, abc                # print(new_prefix)        _permutation_repeat(text, new_prefix, n, k-1)    # print('---')def permutation_repeat(text, k):    _permutation_repeat(text, "", len(text), k)permutation_repeat("abc", 3)

The combination is generated in the following sequence.

a ->
  aa ->
    aaa
    aab
    aac
  ab ->
    aba
    abb
    abc
  ac ->
    aca
    acb
    acc
b ->
  ba ->
    baa
    bab
    bac
  ...
...

Output

aaa
aab
aac
aba
abb
abc
aca
acb
acc
baa
bab
bac
bba
bbb
bbc
bca
bcb
bcc
caa
cab
cac
cba
cbb
cbc
cca
ccb
ccc

Permutation with repeats in result is actually Cartesian Product.

You can use Python itertools.product to generate the same result.

from itertools import productfor _set in product(list('abc'), repeat=3):    print(''.join(_set))

References: